MIPLIB 2010


Hard problems

[Return to complete MIPLIB 2010 problem list]

Click here for legend of abbreviations and links to subsets

Status Name Sets C Rows Cols NZs Int Bin Con Objective AGG VBD PAR PAC COV CAR EQK BIN IVK KNA IKN M01 GEN
Hard b2c1s1 C MBP 3904 3872 11408 288 3584 25687.9X X                   X  
Hard bg512142 C MBP 1307 792 3953 240 552 184203X X                   X  
Hard d10200 C IP 947 2000 57637 1267 733 12430    X           X X      
Hard dc1c C MBP 1649 10039 121158 8380 1659 1.7679e+06X               X     X  
Hard dg012142 C MBP 6310 2080 14795 640 1440 2.30087e+06X X                   X  
Hard dolom1 C MBP 1803 11612 190413 9720 1892 6.60925e+06                X     X  
Hard g200x740i C MBP 940 1480 2960 740 740 30086  X                   X  
Hard ger50_17_trans CU MIP 499 22414 172035 18062 4352 7393.26                      X X
Hard germany50-DBM C MIP 2526 8189 24479 88 8101 473840X                     X X
Hard gmut-75-50 C MBP 2565 68865 571475 68859 6 -1.41807e+07  X   X               X  
Hard gmut-77-40 C MBP 2554 24338 159902 24332 6 -1.4172e+07  X   X               X  
Hard hanoi5 CRBP 16399 3862 39718 3862 1931  X     X       X        
Hard in CRX MBP 1526202 1449074 6811639 1489 1447585 58X X                   X  
Hard ivu52 CRBP 2116 157591 2179476 157591 481.007    X           X X   X  
Hard janos-us-DDM C MIP 760 2184 6384 84 2100 1.49271e+06X                     X X
Hard lrsa120 C MIP 14521 3839 39956 119 120 3600 Infeasible X X             X     X X
Hard mkc C MBP 3411 5325 17038 5323 2 -563.846  X   X         X     X  
Hard n3-3 C MIP 2425 9028 35380 366 8662 15915X                     X X
Hard neos-1140050 CU MBP 3795 40320 808080 38640 1680 Infeasible     X                 X  
Hard neos-807456 CBP 840 1635 4905 1635 Infeasible X   X                    
Hard neos-847302 T MBP 609 737 9566 729 8 4  X X X               X  
Hard neos-948126 R MBP 7271 9551 38219 6965 2586 2607  X   X         X     X  
Hard neos-984165 CR MBP 6962 8883 36742 6478 2405 2188  X   X         X     X  
Hard ns1111636 CR MBP 13895 360822 568444 13200 347622 162      X   X     X X   X  
Hard ns2122603 U MBP 24754 19300 77044 7588 11712 7.77001e+07  X                   X  
Status Name Sets C Rows Cols NZs Int Bin Con Objective AGG VBD PAR PAC COV CAR EQK BIN IVK KNA IKN M01 GEN
Hard nu120-pr3 C IP 2210 8601 25986 61 8540 28130X X X     X             X
Hard opm2-z12-s14 CRBP 319508 10800 725376 10800 -64291  X               X      
Hard opm2-z12-s7 CRBP 319508 10800 725385 10800 -65514  X               X      
Hard p100x588b C MBP 688 1176 2352 588 588 47878  X                   X  
Hard p6b CBP 5852 462 11704 462 -63  X                      
Hard probportfolio C MBP 302 320 6620 300 20 16.7342                X     X  
Hard protfold RBP 2112 1835 23491 1835 -31    X X X X     X     X  
Hard queens-30 CBP 960 900 93440 900 -40                  X      
Hard r80x800 C MBP 880 1600 3200 800 800 5332  X                   X  
Hard rail03 CRBP 253905 758775 1728451 758775 -867.094X X X X   X       X      
Hard reblock354 CBP 19906 3540 52901 3540 -3.92805e+07  X               X      
Hard rmatr200-p10 C MBP 35055 35254 105362 200 35054 2017          X           X  
Hard rmatr200-p20 C MBP 29406 29605 88415 200 29405 837          X           X  
Hard rmine10 CBP 65274 8439 162264 8439 -1913.88  X                   X  
Hard satellites3-40 CUR MBP 44804 81681 698176 79961 1720 -25X X X X   X     X     X  
Hard sct32 C MIP 5440 9767 109654 1332 6396 2039 -17.8876  X             X X   X  
Hard set3-10 C MBP 3747 4019 13747 1424 2595 185179  X                   X  
Hard set3-15 C MBP 3747 4019 13747 1424 2595 124886  X                   X  
Hard set3-20 C MBP 3747 4019 13747 1424 2595 159463  X                   X  
Hard seymour-disj-10 CBP 5108 1209 64704 1209 287  X     X       X     X  
Hard shs1023 C MIP 133944 444625 1044725 440899 1296 2430 13136.6X X   X             X   X
Hard stp3d CRBP 159488 204880 662128 204880 493.72  X X X   X              
Hard swath C MBP 884 6805 34965 6724 81 467.407    X     X           X  
Hard triptim2 CR MIP 14427 27326 521898 6548 20771 7 12.0051X X X X X X     X       X
Hard tw-myciel4 C IP 8146 760 27961 1 759 10X X     X       X       X
Status Name Sets C Rows Cols NZs Int Bin Con Objective AGG VBD PAR PAC COV CAR EQK BIN IVK KNA IKN M01 GEN
Hard uc-case3 C MBP 52003 37749 273618 11256 26493 7204.92X X                   X  
Hard usAbbrv-8-25_70 C MBP 3291 2312 9628 1681 631 120  X     X       X     X  
Hard wnq-n100-mw99-14 CTBP 656900 10000 1333400 10000 259  X     X       X        
Hard zib02 CIXBP 9049868 37709944 146280582 37709944 Infeasible   X X X   X              
Status Name Sets C Rows Cols NZs Int Bin Con Objective AGG VBD PAR PAC COV CAR EQK BIN IVK KNA IKN M01 GEN

Legend

Problem Status

Easy Easy - instance can be solved within one hour using a commercial solver
Hard Hard - instance has been solved, but is not considered easy
Open Open - optimal solution to instance is unknown

Instance Set List

BBenchmark set
CChallenge set
IInfeasible set
PPrimal set
UUnstable set
R Reoptimize set
T Tree set
XXXL - extra large instances

Problem Type List

BPBinary Program - All variables are binary
IP Integer Program - All variables are integer
MBP Mixed Binary Program - All variables are binary or continuous
MIPMixed Integer Program - Variables can be integer or continuous

Note: The problem types are used to partition the instances. Instances that match more than one type are grouped into the least general set.

Problem Feasibility List

Feasible Problems - a feasible solution is known
Infeasible Problems - the problem was proven to be infeasible
Unknown Feasiblility - no feasible solution is know, but the problem was not proven to be infeasible

Constraint Type Legend

AGGAggregation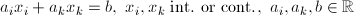
VBDVariable Bound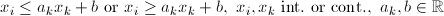
PARSet Partition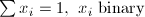
PACSet Packing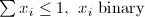
COVSet Cover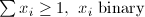
CARCardinality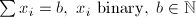
EQKEquality Knapsack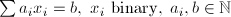
BINBin Packing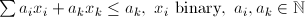
IVKInvariant Knapsack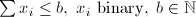
KNAKnapsack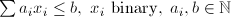
IKNInteger Knapsack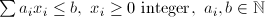
M01Mixed Binary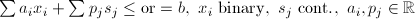
GENGeneralAll other constraint types

Note: If a constraint matches more than one type, it is counted for the one with highest priority (lowest number).
Scaling and negation of binary are applied to match constraint types.

Last Update July 31, 2019 by Gerald Gamrath
© 2019 by Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB)
Imprint