MIPLIB 2010

Infeasible set

[Return to complete MIPLIB 2010 problem list]

Click here for legend of abbreviations and links to subsets

Status	Name	Sets	C	Rows	Cols	NZs	Int	Bin	Con	Objective	AGG	VBD	PAR	PAC	COV	CAR	EQK	BIN	IVK	KNA	IKN	M01	GEN
	ash608gpia-3col	B I	BP	24748	3651	74244		3651		Infeasible			X	X
	enlight14	B I	IP	196	392	1120	196	196		Infeasible													X
	enlight16	I T	IP	256	512	1472	256	256		Infeasible													X
	enlight9	I	IP	81	162	450	81	81		Infeasible													X
	neos-785912	I	BP	1714	1380	16610		1380		Infeasible		X		X					X
	neos788725	I	BP	433	352	4912		352		Infeasible		X	X						X			X
	neos-820146	I T	BP	830	600	3225		600		Infeasible				X	X	X			X
	neos-820157	I T	BP	1015	1200	4875		1200		Infeasible		X	X	X	X	X			X
	neos858960	I T	BP	132	160	2770		160		Infeasible		X				X			X
	neos-859770	I	BP	2065	2504	880736		2504		Infeasible			X						X			X
	ns1158817	I	MBP	68455	1804022	2842044		66022	1738000	Infeasible				X		X			X	X		X
	ns1686196	I	BP	4055	2738	68529		2738		Infeasible		X	X	X		X			X	X		X
	ns1702808	I	MBP	1474	804	5856		666	138	Infeasible			X			X						X
	ns1745726	I	BP	4687	3208	90278		3208		Infeasible		X	X	X		X			X	X		X
	ns1766074	B I T	MIP	182	100	666	90		10	Infeasible											X		X
	ns1769397	I	BP	5527	3772	117383		3772		Infeasible		X	X	X		X			X	X		X
	ns2118727	I R	MBP	163354	167440	646864		159514	7926	Infeasible		X			X				X			X
	p2m2p1m1p0n100	I T	BP	1	100	100		100		Infeasible										X		X
	zib02	C I X	BP	9049868	37709944	146280582		37709944		Infeasible		X	X	X		X
Status	Name	Sets	C	Rows	Cols	NZs	Int	Bin	Con	Objective	AGG	VBD	PAR	PAC	COV	CAR	EQK	BIN	IVK	KNA	IKN	M01	GEN

Legend

Problem Status

Easy Easy - instance can be solved within one hour using a commercial solver
Hard Hard - instance has been solved, but is not considered easy
Open Open - optimal solution to instance is unknown

Instance Set List

B	Benchmark set
C	Challenge set
I	Infeasible set
P	Primal set
U	Unstable set
R	Reoptimize set
T	Tree set
X	XXL - extra large instances

Problem Type List

BP	Binary Program - All variables are binary
IP	Integer Program - All variables are integer
MBP	Mixed Binary Program - All variables are binary or continuous
MIP	Mixed Integer Program - Variables can be integer or continuous

Note: The problem types are used to partition the instances. Instances that match more than one type are grouped into the least general set.

Problem Feasibility List

Feasible Problems - a feasible solution is known
Infeasible Problems - the problem was proven to be infeasible
Unknown Feasiblility - no feasible solution is know, but the problem was not proven to be infeasible

Constraint Type Legend

AGG	Aggregation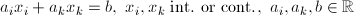
VBD	Variable Bound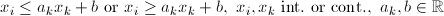
PAR	Set Partition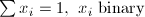
PAC	Set Packing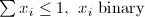
COV	Set Cover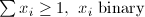
CAR	Cardinality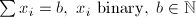
EQK	Equality Knapsack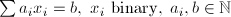
BIN	Bin Packing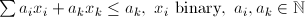
IVK	Invariant Knapsack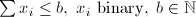
KNA	Knapsack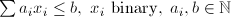
IKN	Integer Knapsack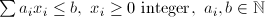
M01	Mixed Binary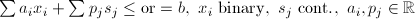
GEN	General	All other constraint types

Note: If a constraint matches more than one type, it is counted for the one with highest priority (lowest number).
Scaling and negation of binary are applied to match constraint types.