Click here for legend of abbreviations and links to subsets
| Status | Name | Sets | C | Rows | Cols | NZs | Int | Bin | Con | Objective | AGG | VBD | PAR | PAC | COV | CAR | EQK | BIN | IVK | KNA | IKN | M01 | GEN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
datt256 | C | BP | 11077 | 262144 | 1503732 | 262144 | ? | X | X | X | ||||||||||||
|
neos-952987 | C | BP | 354 | 31329 | 90384 | 31329 | ? | X | X | X | X | |||||||||||
 |
ns1778858 | C | BP | 10666 | 4720 | 32673 | 4720 | -2.26357e+07 | X | X | X | X | |||||||||||
|
ns1905800 | C | MIP | 8289 | 3228 | 38100 | 3 | 3030 | 195 | ? | X | X | X | X | X | ||||||||
|
zib01 | CX | BP | 5887041 | 12471400 | 49877768 | 12471400 | ? | X | X | X | ||||||||||||
| Status | Name | Sets | C | Rows | Cols | NZs | Int | Bin | Con | Objective | AGG | VBD | PAR | PAC | COV | CAR | EQK | BIN | IVK | KNA | IKN | M01 | GEN |
Easy -
instance can be solved within one hour using a commercial solver
Hard -
instance has been solved, but is not considered easy
Open -
optimal solution to instance is unknown
| B | Benchmark set |
| C | Challenge set |
| I | Infeasible set |
| P | Primal set |
| U | Unstable set |
| R | Reoptimize set |
| T | Tree set |
| X | XXL - extra large instances |
| BP | Binary Program - All variables are binary |
| IP | Integer Program - All variables are integer |
| MBP | Mixed Binary Program - All variables are binary or continuous |
| MIP | Mixed Integer Program - Variables can be integer or continuous |
Note: The problem types are used to partition the instances. Instances that match more than one type are grouped into the least general set.
Feasible Problems - a feasible solution is known
Infeasible Problems - the problem was proven to be infeasible
Unknown Feasiblility - no feasible solution is know, but the problem was not proven to be infeasible
| AGG | Aggregation |  |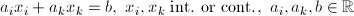
|---|---|---|
| VBD | Variable Bound |  |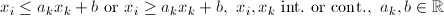
| PAR | Set Partition |  |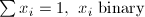
| PAC | Set Packing |  |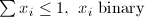
| COV | Set Cover |  |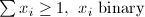
| CAR | Cardinality |  |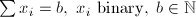
| EQK | Equality Knapsack |  |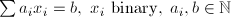
| BIN | Bin Packing |  |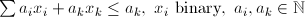
| IVK | Invariant Knapsack |  |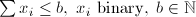
| KNA | Knapsack |  |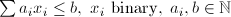
| IKN | Integer Knapsack |  |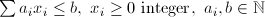
| M01 | Mixed Binary |  |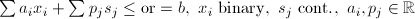
| GEN | General | All other constraint types |
Note: If a constraint matches more than one type, it is counted for the one
with highest priority (lowest number).
Scaling and negation of binary are
applied to match constraint types.