MIPLIB 2010

Unstable set

[Return to complete MIPLIB 2010 problem list]

Click here for legend of abbreviations and links to subsets

Status	Name	Sets	C	Rows	Cols	NZs	Int	Bin	Con	Objective	AGG	VBD	PAR	PAC	COV	CAR	EQK	BIN	IVK	KNA	IKN	M01	GEN
	cdma	C U	MBP	9095	7891	168227		4235	3656	?	X	X		X	X			X	X			X
	ger50_17_trans	C U	MIP	499	22414	172035	18062		4352	7393.26												X	X
	harp2	U	BP	112	2993	5840		2993		-7.38998e+07			X							X		X
	hawaiiv10-130	C U X	MBP	1388052	685130	183263061		578444	106686	?	X	X	X	X		X			X			X
	momentum2	U	MIP	24237	3732	349695	1	1808	1923	12314.1		X	X						X			X	X
	nb10tb	C U	MIP	150495	73340	1172289	2756	14124	56460	?	X	X		X				X	X	X		X
	neos-1112782	U	MBP	2115	4140	8145		2070	2070	5.72103e+11		X										X
	neos-1112787	U	MBP	1680	3280	6440		1640	1640	5.65032e+11		X										X
	neos-1140050	C U	MBP	3795	40320	808080		38640	1680	Infeasible			X									X
	neos-1225589	U	MBP	675	1300	2525		650	650	1.23107e+09		X										X
	neos-520729	U	MBP	31178	91149	322203		30708	60441	-1.385e+06	X		X									X
	neos-799711	U	MBP	59218	41998	147164		910	41088	-1.11702e+07	X	X		X		X						X
	npmv07	U	MBP	76342	220686	859614		1880	218806	1.0481e+11		X										X
	ns2017839	U	MBP	54510	55224	317840		12	55212	7.70305e+13	X	X										X
	ns2122603	U	MBP	24754	19300	77044		7588	11712	7.77001e+07		X										X
	ofi	U	MIP	422587	420434	1778754	11073	18632	390729	6.15538e+09	X	X	X									X
	satellites2-60	C U R	MBP	20916	35378	283668		34324	1054	-19	X	X	X	X		X			X			X
	satellites3-40-fs	C U R	MBP	35553	81681	291161		79961	1720	-25	X	X	X	X		X						X
	satellites3-40	C U R	MBP	44804	81681	698176		79961	1720	-25	X	X	X	X		X			X			X
	splan1	C U X	MIP	572800	1317382	5233840	1978	90810	1224594	?	X	X		X		X			X	X	X	X	X
	transportmoment	C U	MBP	9616	9685	29541		2456	7229	-3.0631e+09	X	X										X
Status	Name	Sets	C	Rows	Cols	NZs	Int	Bin	Con	Objective	AGG	VBD	PAR	PAC	COV	CAR	EQK	BIN	IVK	KNA	IKN	M01	GEN

Legend

Problem Status

Easy Easy - instance can be solved within one hour using a commercial solver
Hard Hard - instance has been solved, but is not considered easy
Open Open - optimal solution to instance is unknown

Instance Set List

B	Benchmark set
C	Challenge set
I	Infeasible set
P	Primal set
U	Unstable set
R	Reoptimize set
T	Tree set
X	XXL - extra large instances

Problem Type List

BP	Binary Program - All variables are binary
IP	Integer Program - All variables are integer
MBP	Mixed Binary Program - All variables are binary or continuous
MIP	Mixed Integer Program - Variables can be integer or continuous

Note: The problem types are used to partition the instances. Instances that match more than one type are grouped into the least general set.

Problem Feasibility List

Feasible Problems - a feasible solution is known
Infeasible Problems - the problem was proven to be infeasible
Unknown Feasiblility - no feasible solution is know, but the problem was not proven to be infeasible

Constraint Type Legend

AGG	Aggregation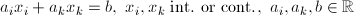
VBD	Variable Bound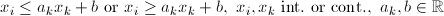
PAR	Set Partition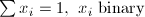
PAC	Set Packing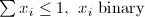
COV	Set Cover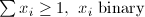
CAR	Cardinality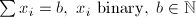
EQK	Equality Knapsack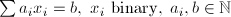
BIN	Bin Packing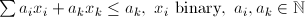
IVK	Invariant Knapsack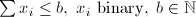
KNA	Knapsack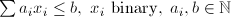
IKN	Integer Knapsack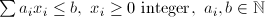
M01	Mixed Binary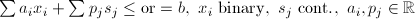
GEN	General	All other constraint types

Note: If a constraint matches more than one type, it is counted for the one with highest priority (lowest number).
Scaling and negation of binary are applied to match constraint types.