
Click here for legend of abbreviations and links to subsets
| Status | Name | Sets | C | Rows | Cols | NZs | Int | Bin | Con | Objective | AGG | VBD | PAR | PAC | COV | CAR | EQK | BIN | IVK | KNA | IKN | M01 | GEN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
30_70_45_095_100 | P | MBP | 12526 | 10976 | 46640 | 10975 | 1 | 3 | X | X | X | X | ||||||||||
 |
acc-tight4 | PR | BP | 3285 | 1620 | 17073 | 1620 | 0 | X | X | X | X | X | X | X | ||||||||
 |
acc-tight5 | BPR | BP | 3052 | 1339 | 16134 | 1339 | 0 | X | X | X | X | X | X | X | X | |||||||
 |
acc-tight6 | PR | BP | 3047 | 1335 | 16108 | 1335 | 0 | X | X | X | X | X | X | X | X | |||||||
 |
bnatt350 | BPR | BP | 4923 | 3150 | 19061 | 3150 | 0 | X | X | X | ||||||||||||
 |
ex10 | P | BP | 69608 | 17680 | 1162000 | 17680 | 100 | X | X | X | ||||||||||||
 |
ex9 | BP | BP | 40962 | 10404 | 517112 | 10404 | 81 | X | X | X | ||||||||||||
 |
lectsched-1 | P | IP | 50108 | 28718 | 310792 | 482 | 28236 | 0 | X | X | X | X | ||||||||||
 |
lectsched-2 | P | IP | 30738 | 17656 | 186520 | 369 | 17287 | 0 | X | X | X | X | ||||||||||
 |
lectsched-3 | P | IP | 45262 | 25776 | 279967 | 457 | 25319 | 0 | X | X | X | X | ||||||||||
 |
m100n500k4r1 | BP | BP | 100 | 500 | 2000 | 500 | -25 | X | ||||||||||||||
 |
neos-1171692 | P | MBP | 4239 | 1638 | 42945 | 819 | 819 | -273 | X | X | X | |||||||||||
 |
neos-1171737 | P | MBP | 4179 | 2340 | 58620 | 1170 | 1170 | -195 | X | X | X | |||||||||||
 |
neos-1224597 | P | IP | 3276 | 3395 | 25090 | 245 | 3150 | -428 | X | X | X | X | X | X | X | X | ||||||
 |
neos-1440225 | P | BP | 330 | 1285 | 14168 | 1285 | 36 | X | ||||||||||||||
 |
neos-506422 | P | MBP | 6811 | 2527 | 31815 | 63 | 2464 | 0 | X | X | X | |||||||||||
 |
neos-555424 | P | IP | 2676 | 3815 | 15667 | 15 | 3800 | 1.2868e+06 | X | X | X | X | X | X | ||||||||
 |
neos-693347 | P | MBP | 3192 | 1576 | 113472 | 1405 | 171 | 234 | X | X | X | X | X | |||||||||
 |
neos6 | P | MBP | 1036 | 8786 | 251946 | 8340 | 446 | 83 | X | X | X | X | X | |||||||||
 |
neos-738098 | P | MBP | 25849 | 9093 | 101360 | 8946 | 147 | -1099 | X | X | X | X | X | X | X | X | ||||||
 |
neos-777800 | P | BP | 479 | 6400 | 32000 | 6400 | -80 | X | X | X | ||||||||||||
 |
neos808444 | P | BP | 18329 | 19846 | 120512 | 19846 | 0 | X | X | X | X | X | X | X | ||||||||
 |
neos-824661 | P | MBP | 18804 | 45390 | 138890 | 15640 | 29750 | 33 | X | X | X | X | ||||||||||
 |
neos-824695 | P | MBP | 9576 | 23970 | 72590 | 8500 | 15470 | 31 | X | X | X | X | ||||||||||
 |
neos-826694 | P | MBP | 6904 | 16410 | 59268 | 16290 | 120 | 58 | X | X | X | X | X | X | ||||||||
| Status | Name | Sets | C | Rows | Cols | NZs | Int | Bin | Con | Objective | AGG | VBD | PAR | PAC | COV | CAR | EQK | BIN | IVK | KNA | IKN | M01 | GEN |
 |
neos-826812 | P | MBP | 6844 | 15864 | 53808 | 10350 | 5514 | 58.011 | X | X | X | X | ||||||||||
 |
neos-849702 | BP | BP | 1041 | 1737 | 19308 | 1737 | 0 | X | X | X | X | |||||||||||
 |
neos-885086 | P | MBP | 11574 | 4860 | 248310 | 2430 | 2430 | -243 | X | X | X | |||||||||||
 |
neos-885524 | P | BP | 65 | 91670 | 258309 | 91670 | 12320.1 | X | ||||||||||||||
 |
neos-932816 | P | MBP | 30823 | 21007 | 484926 | 20566 | 441 | 15376 | X | X | X | X | ||||||||||
 |
neos-933638 | P | MBP | 13658 | 32417 | 187173 | 28637 | 3780 | 276 | X | X | X | X | ||||||||||
 |
neos-933966 | P | MBP | 12047 | 31762 | 180618 | 27982 | 3780 | 318 | X | X | X | X | ||||||||||
 |
neos-935627 | PR | MBP | 7859 | 10301 | 40476 | 7522 | 2779 | 2598 | X | X | X | X | ||||||||||
 |
neos-935769 | P | MBP | 6741 | 9799 | 36447 | 7020 | 2779 | 3010 | X | X | X | X | ||||||||||
 |
neos-937511 | P | MBP | 8158 | 11332 | 44237 | 8562 | 2770 | 3510 | X | X | X | X | ||||||||||
 |
neos-941313 | P | BP | 13189 | 167910 | 484080 | 167910 | 9361 | X | X | X | X | X | X | X | ||||||||
 |
neos-957389 | P | BP | 5115 | 6036 | 355372 | 6036 | 1.5 | X | X | X | X | X | X | |||||||||
 |
ns1116954 | P | MBP | 131991 | 12648 | 410582 | 7482 | 5166 | 0 | X | X | X | X | X | X | X | |||||||
 |
ns1952667 | P | IP | 41 | 13264 | 335643 | 13264 | 0 | X | X | |||||||||||||
 |
triptim1 | BP | MIP | 15706 | 30055 | 515436 | 9597 | 20451 | 7 | 22.8681 | X | X | X | X | X | X | |||||||
| Status | Name | Sets | C | Rows | Cols | NZs | Int | Bin | Con | Objective | AGG | VBD | PAR | PAC | COV | CAR | EQK | BIN | IVK | KNA | IKN | M01 | GEN |
 Easy -
instance can be solved within one hour using a commercial solver
Easy -
instance can be solved within one hour using a commercial solver
 Hard -
instance has been solved, but is not considered easy
Hard -
instance has been solved, but is not considered easy
 Open -
optimal solution to instance is unknown
Open -
optimal solution to instance is unknown
| B | Benchmark set |
| C | Challenge set |
| I | Infeasible set |
| P | Primal set |
| U | Unstable set |
| R | Reoptimize set |
| T | Tree set |
| X | XXL - extra large instances |
| BP | Binary Program - All variables are binary |
| IP | Integer Program - All variables are integer |
| MBP | Mixed Binary Program - All variables are binary or continuous |
| MIP | Mixed Integer Program - Variables can be integer or continuous |
Note: The problem types are used to partition the instances. Instances that match more than one type are grouped into the least general set.
Feasible Problems - a feasible solution is known
Infeasible Problems - the problem was proven to be infeasible
Unknown Feasiblility - no feasible solution is know, but the problem was not proven to be infeasible
| AGG | Aggregation | 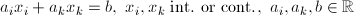 |
|---|---|---|
| VBD | Variable Bound | 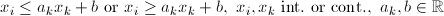 |
| PAR | Set Partition | 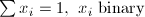 |
| PAC | Set Packing | 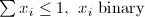 |
| COV | Set Cover | 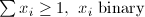 |
| CAR | Cardinality | 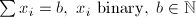 |
| EQK | Equality Knapsack | 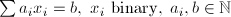 |
| BIN | Bin Packing | 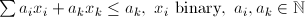 |
| IVK | Invariant Knapsack | 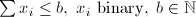 |
| KNA | Knapsack | 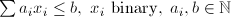 |
| IKN | Integer Knapsack | 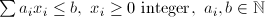 |
| M01 | Mixed Binary | 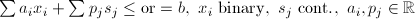 |
| GEN | General | All other constraint types |
Note: If a constraint matches more than one type, it is counted for the one
with highest priority (lowest number).
Scaling and negation of binary are
applied to match constraint types.